3 4 5 треугольник

Строительство с применением египетского треугольника древний способ, активно используемый до сих пор современными строителями. Название получил благодаря древнеегипетским сооружениям, хотя известно, что история его начинается задолго до этого периода.

Но, скорее всего, свойства уникальной фигуры не были оценены в те времена, пока не появился Пифагор, сумевший проанализировать и оценить изящные формы фигуры.

Египетский треугольник известен еще с древних времен. Он был и остается популярен в строительстве и архитектуре много веков.

Считается, что создал геометрическую конструкцию великий греческий математик Пифагор Самосский. Благодаря ему сегодня мы можем использовать все свойства геометрической постройки в области строения.

Египетский треугольник в строительстве. Общие сведения

Зарождение идеи

Идея у математика появилась после путешествия в Африку по просьбе Фалеса, который поставил задачу Пифагору изучить математику и астрономию тех мест. В Египте он среди бескрайней пустыни встретил величественные строения, поразившие его размером, изяществом и красотой.

Надо заметить, что более двух с половиной тысяч лет назад пирамиды были несколько другими – огромными, с четкими гранями. Тщательно изучив могущественные постройки, коих было не мало, так как рядом с великанами, стояли храмы поменьше, построенные для детей, жен и других родственных лиц фараона, это натолкнуло его на мысль.

Благодаря своим математическим способностям, Пифагор сумел определить закономерность в формах пирамиды, а умение анализировать и делать выводы привели к созданию одной из самых значимых теорий в истории геометрии.

Из истории

Знали ли в древнем Египте о геометрии и математике? Конечно да. Жизнь египтян была тесно связана с наукой. Они регулярно пользовались знаниями при разметке полей, создании архитектурных шедевров. Даже существовала своя служба землемеров, которые применяли геометрические правила, занимаясь восстановлением границ.

Название треугольник получил благодаря эллинам, которые нередко бывали в Египте в VII-V вв. до н.э. Считается, что прообразом фигуры стала пирамида Хеопса, отличающаяся совершенными пропорциями. Ее место особенное в истории. Если посмотреть поперечное сечение, то можно отметить два треугольника, у которых угол внутри равняется 51о50’.

Строение

Сегодня это строение усеченной формы, приобретенной под воздействием времени, высота явно потерялась. Однако, восстановив ее геометричность, можно сделать вывод, что стороны треугольников равны. Получается в основе заложен золотой прямоугольный треугольник.

Однако, следует рассмотреть другую пирамиду – Хефрена, у которой основа как раз-таки прямоугольный треугольник и где угол наклона боковых граней равен 53о12 с соотношением катетов 4:3. Это уже так называемый священный треугольник. Для египтян такая фигура сопоставлялась с семейным очагом: катет вертикального положения олицетворял мужчину, основание – представительницу прекрасного пола, а гипотенуза – рождение ребенка от обоих.

Стороны пирамиды Хефрена в соотношении равны 3:4:5, что точно соответствует теореме Пифагора. Значит, можно сделать вывод, что строители уже знали об этой теореме, но не могли ее сформулировать. Хотя, в исторических письменах встречаются следы использования египетского треугольника за много веков даже до Египта. До сегодняшнего дня это загадка, как могли такие знания получить древние египтяне. Понимали ли они чем обладают?

Особенность фигуры к тому же в том, что благодаря подобному соотношению, она является простым и первым Героновым треугольником, так как ее стороны и площадь целочисленные.

Обратное доказательство

Как доказать, что треугольник прямоугольный? Нужно порой исходить от обратного, то есть если сумма квадратов обеих сторон равна квадрату третьей, то треугольник прямоугольный, что подтверждает равенство 32х42=52 и значит он действительно прямоугольный.

Таким образом теорема Пифагора стала каноном и фундаментом развития математической науки. Со школьной скамьи каждый ученик знает, что означает выражение «Пифагоровы штаны во все стороны равны».

Интересно, что теорема Пифагора находится в Книге Гиннесса как теорема, обладающая самым большим количеством доказательств, которых примерно 500.

Особенности

Если рассмотреть более детально отличительные особенности египетского треугольника, то можно выделить следующие моменты:

• все стороны и площадь состоят из целых чисел, как говорилось выше;
• согласно теории великого математика, сумма квадратов катетов равна квадрату гипотенузе;
• такой фигурой возможно отмерить прямые углы в пространстве. Это используется в процессе строительства до сих пор;
• не обязательно пользоваться специальными измерительными приборами, подойдут подручные средства, например, веревка.

Место в строительном мире

С древнейших времен египетский треугольник нашел почетное место в архитектуре и строительстве. Конструкция пирамиды отличается тем, что позволяет создавать здание с совершенно правильными углами без каких-либо дополнительных инструментов.

Задача намного облегчается, если использовать транспортир или треугольник. Но, раньше применялись только шнуры и веревке, разделенные на отрезки. Благодаря отметкам на веревке можно было с точностью воссоздать прямоугольную фигуру. Строителям заменяла транспортир и угольник веревка, для чего отмечали узлами на ней 12 частей и складывали треугольник с отрезками 3,4,5. Прямой угол получался без затруднений. Эти знания помогли создать множество сооружений, в том числе пирамиды.

Интересно, что до древнего Египта, таким способом строили в Китае, Вавилоне, Месопотамии.

Свойства египетской треугольной фигуры подчиняются истине – квадрат гипотенузы равен квадратам двух катетов. Эта теорема Пифагора знакома каждому со школьной поры. Например, умножаем 5х5 и получаем гипотенузу равную числу 25. Квадраты обоих катетов равны 16 и 9, что в сумме дает цифру 25.

Благодаря таким свойствам, треугольник нашел применение в строительстве. Можно взять любую деталь, с целью провести линию прямого направления с условием, что ее длина должна быть кратной пяти. После этого заметить один край и прочертить от него линию кратную четырем, а от другого кратную трем. При этом каждый отрезок должен быть длиной минимум четыре и три. Пересекаясь, они образовывают один прямой угол в 90 градусов. Другие углы равны 53,13 и 36,87 градусам.

Какие существуют альтернативные варианты

Как создать прямой угол

Лучшим вариантом смастерить прямой угол является применение угольника или транспортира. Это позволит с минимальными затратами найти необходимые пропорции. Но, основной момент египетского треугольника в его универсальности из-за возможности создать фигуру, не имея под рукой ничего.

В этом деле может пригодиться все, даже печатные издания. Любая книга или даже журнал имеют всегда соотношение сторон, образующее прямой угол. Типографские станки работают всегда точно, чтобы рулон, заправленный в машину резался пропорциональными углами.

Древние инженеры придумывали много способов строительства египетского треугольника и всегда экономили ресурсы.

Поэтому, самым простым и широко применяемым был метод постройки геометрической фигуры с применением обычной веревки. Бралась бечевка и резалась на 12 ровных частей, из которых выкладывалась фигура с пропорциями 3,4 и 5.

Как создать другие углы?

Египетский треугольник в строительном мире нельзя недооценивать. Его свойства однозначно полезны, но без возможности построить углы другого градуса в строительстве невозможно. Чтобы образовался угол в 45 градусов, понадобится рамка или багет, которые распиливаются под углом в 45 градусов и соединяются между собой.

Важно! Чтобы получить необходимый наклон, потребуется позаимствовать бумажный лист из печатного издания и согнуть его. Линии изгиба при этом будут проходить через угол. Края должны быть соединены.

Получить 60 градусов можно с применением двух треугольников по 30 градусов. Чаще всего используются для создания декоративных элементов.

Небольшие хитрости

Египетский треугольник 3х4х5 актуален для маленьких домов. Но, что делать, если дом 12х15?

Для этого нужно построить прямоугольный треугольник, у которого катеты равняются 12 и 15 м. Гипотенуза находится как квадратный корень из суммы 12х12 и 15х15. В итоге получаем 19,2 м. С помощью чего-либо — веревки, шпагата, бечевки, тросика, военного кабеля, отмеряем 12, 15 и 19,2 м. Делаем узлы на этих местах и ставим жимки.

Затем треугольник нужно растянуть на нужном месте и установить 3 точки опоры, в которые вбить колышки. Четвертую точку можно получить, не трогая концы катетов. Для этого точка прямого угла перекидывается по диагонали и все готово.

Например, есть участок, где требуется прямой угол – для места под кухонный гарнитур, раскладки кафеля и других моментов. Хорошо бы такие вопросы учесть при кладке, но реальность другая и не всегда попадаются ровные стены и прямые углы. Здесь пригодится египетский треугольник с соотношением 3:4:5, либо при необходимости 1,5:2:2,5.

Обязательно учитывается толщина маяков, погрешность, бугры на стенах и т.д. Треугольник рисуется с помощью рулетки и мела. Если разметка небольшая, то можно воспользоваться листом гипсокартона, так как режутся они с правильными углами.

Египетский треугольник широко использовался в строительстве целых 2,5 века. И сегодня иногда приходится применять данную методику, при отсутствии необходимых инструментов, чтобы получить прямые углы. Свойства этой фигуры уникальны, что гарантирует точность в архитектуре и строительстве, без которой не обойтись. С ним легко работать, по форме он гармоничен и красив. До сих пор пытливые умы пытаются разгадать тайну египетского треугольника.

Египетский треугольник

Смотреть что такое «Египетский треугольник» в других словарях:

• Египетский треугольник — – прямоугольный треугольник с соотношением сторон 3:4:5. Сумма указанных чисел (3+4+5=12) с древних времен использовалась как единица кратности при построении прямых углов с помощью веревки, размеченной узлами на 3/12 и 7/12 ее длины. Применялся… … Словарь строителя

• Египетский треугольник — прямоугольный треугольник с отношением сторон 3:4:5 (сумма чисел 3 + 4 + 5 = 12). Землемеры и архитекторы с глубокой древности пользовались соотношением этих чисел для построения прямых углов с помощью верёвки, размеченной узлами на 3/12 и… … Архитектурный словарь

• Египетский Треугольник — Прямоугольный треугольник с соотношением сторон 3:4:5. Сумма указанных чисел (3+4+5=12) с древних времен использовалась как единица кратности при построении прямых углов с помощью веревки, размеченной узлами на 3/12 и 7/12 ее длины. Применялся в… … Строительный словарь

• лунный египетский треугольник — Треугольник, возникающий в центре большого квадрата, построенного на базе трёх лунных обелисков с отношением сторон 3:4:5, при условии, что вся площадь квадрата разделена на серию прямоугольных треугольников с отношением катетов 1:2. E. Egyptian… … Толковый уфологический словарь с эквивалентами на английском и немецком языках

• Треугольник (значения) — В Викисловаре есть статья «треугольник» Треугольник в широком смысле объект треугольной формы, либо тройка объектов, попарно связ … Википедия

• Треугольник Халаиба — Халаибский треугольник مثلث حلايب спорная территория ← … Википедия

• Египетский крест (астеризм) — В этой статье не хватает ссылок на источники информации. Информация должна быть проверяема, иначе она может быть поставлена под сомнение и удалена. Вы можете … Википедия

• Египетский лук — Угловой лук у стрелка на колеснице и простой у пехотинца Египетские луки, как стрелковое оружие прошли определенный путь эволюционного развития от простого из одного вида дерева до сложносоставного («углового») из разных видов… … Википедия

• Халаибский треугольник — مثلث حلايب спорная территория ← … Википедия

• Зимний треугольник — красный цвет = зимний треугольник, синий цвет = зимний круг … Википедия

Египетский треугольник, его свойства

О египетском треугольнике и его свойствах хорошо известно ещё с древних времён. Эта фигура широко применялась в строительстве для разметки и построения правильных углов.

История египетского треугольника

Создателем этой геометрической конструкции является один из величайших математиков древности Пифагор. Именно благодаря его математическим изысканиям мы можем в полной мере использовать все свойства данного геометрического построения в строительстве.

Важно! Принято считать, что толчком к открытию этой геометрической фигуры послужило путешествие Пифагора в Африку, где он увидел египетские пирамиды. Возможно, именно они стали прообразом данной конструкции.

Можно предположить, что математические навыки позволили Пифагору заметить закономерность в формах строения. Дальнейшее развитие событий можно легко представить. Базовый анализ и построение выводов создали одну из самых значимых фигур в истории. Скорее всего, в качестве прообраза была выбрана именно пирамида Хеопса из-за своих практически совершенных пропорций.

Египетский треугольник в строительстве

Свойства этой уникальной геометрической конструкции заключаются в том, что её построение без применения каких-либо инструментов позволяет построить дом с правильными во всех соотношениях углами.

Важно! Конечно, в идеале лучшим вариантом будет использование транспортира или угольника.

Итак, качества египетского треугольника позволяют делать правильные во всех соотношениях углы. Стороны конструкции имеют следующее соотношение друг к другу:

1. 5,
2. 4,

Чтобы проверить ту ли фигуру вы начертили, используйте хорошо известную ещё со школьной скамьи Теорему Пифагора.

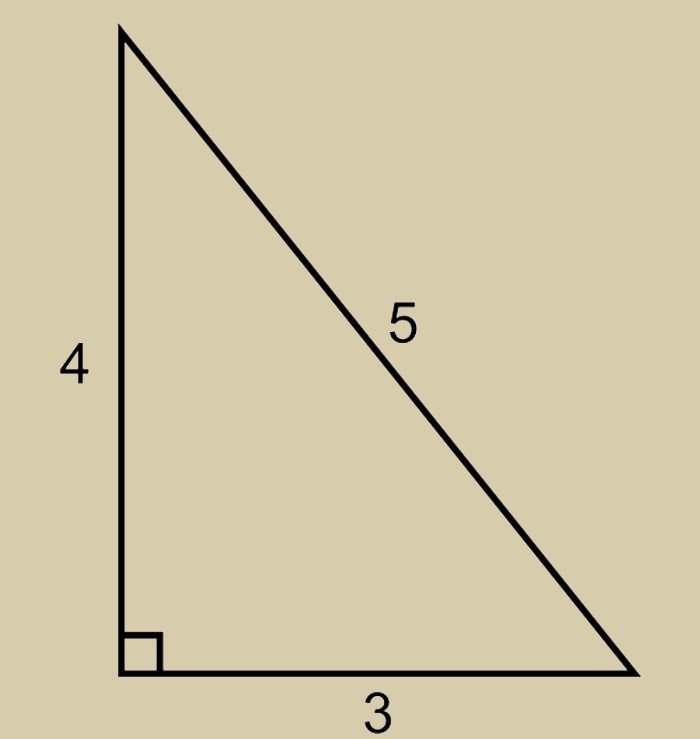
Внимание! Свойства египетского треугольника таковы, что квадрат гипотенузы равен квадратам двух катетов.

Для лучшего понимания возьмём приведенную выше зависимость и составим небольшой пример. Умножим пять на пять. В результате чего получим гипотенузу равную 25. Вычислим квадраты двух катетов. Они составят 16 и 9. Соответственно их сумма будет двадцать пять.

Именно поэтому свойства египетского треугольника так часто используются в строительстве. Вам достаточно взять заготовку и прочертить прямую линию. Её длина всегда должна быть кратной 5. Затем нужно наметить один край и отмерять от него линию кратную 4, а от второго 3.

Внимание! Длина каждого отрезка составит 4 и 3 см (при минимальных значениях). Пересечение этих прямых образует прямой угол, равняющийся 90 градусам.

Альтернативные способы построить прямой угол на 90 градусов

Как уже упоминалось выше, наилучшим вариантом будет просто взять угольник или транспортир. Эти инструменты позволяют с наименьшими затратами времени и сил добиться нужных пропорций. Главное же свойство египетского треугольника заключается в его универсальности. Фигуру можно построить, не имея в арсенале практически ничего.

Сильно в построении прямого угла помогают простые печатные издания. Возьмите любой журнал или книгу. Дело в том, что в них соотношение сторон всегда составляет ровно 90 градусов. Типографические станки работают очень точно. В противном случае рулон, который заправляется в станок, будет резаться непропорциональными кривыми углами.

Как получить египетский треугольник при помощи верёвки

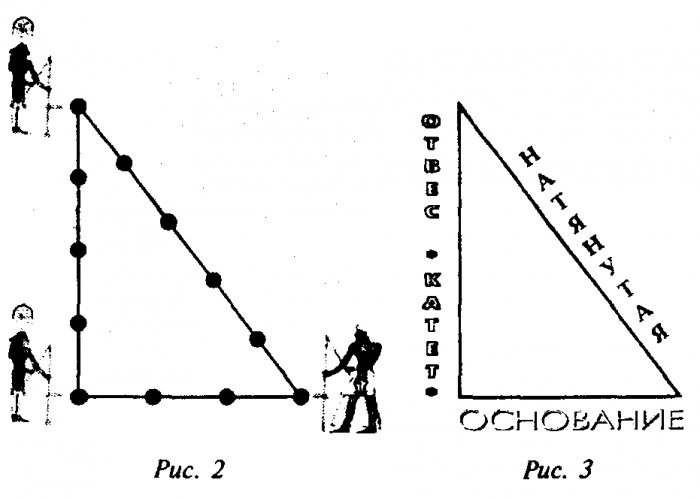
Свойства этой геометрической фигуры тяжело переоценить. Неудивительно, что инженерами древности было придумано множество способов её образования с использованием минимальных ресурсов.

Одним из самых простых считается метод образования египетского треугольника со всеми его вытекающими свойствами посредством простой верёвки. Возьмите бечёвку и разрежьте её на 12 абсолютно ровных частей. Из них сложите фигуру с пропорциями 3, 4 и 5.

Как построить угол в 45, 30 и 60 градусов

Безусловно, египетский треугольник и его свойства очень полезны при постройке дома. Но без других углов вам обойтись всё-таки не удастся. Чтобы получить угол, равняющийся 45 градусам, возьмите материал рамки или багета. После чего распилите его под углом в сорок пять градусов и состыкуйте половинки друг с другом.

Важно! Для получения нужного наклона вырвите лист бумаги из журнала и согните его. При этом линии изгиба будут проходить через угол. Края должны совпасть.

Как видите, свойства фигуры позволяют гораздо проще и быстрее построить геометрический конструкт. Чтобы добиться соотношения сторон в 60 градусов нужно взять один треугольник на 30º и второй такой же. Обычно подобные пропорции необходимы при создании определённых декоративных элементов.

Внимание! Соотношение сторон на 30º нужно, чтобы сделать шестиугольники. Их свойства востребованы в столярных заготовках.

Итоги

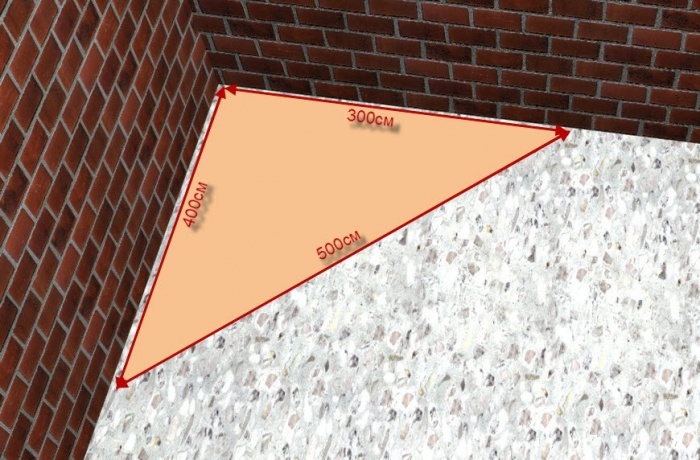
Свойства египетского треугольника широко использовались в строительстве на протяжении почти, что двух с половиной веков. Даже сейчас при недостатке инструментов строители применяют эту открытую ещё Пифагором методику, чтобы добиться ровных прямых углов.

Конспект урока геометрии «Египетский треугольник »

Выполнила:

Бусева О.А.

Учитель математики

Конспект урока геометрии «Египетский треугольник «

ТЕМА » ТЕОРЕМА ПИФАГОРА»

Цели урока:

Образовательная – изучить теорему Пифагора, создав проблемную ситуацию и решить проблему, используя практические навыки работы с моделями, научить учащихся применять теорему при решении задач,

Воспитательная – развитие интереса к математике через знакомство с деятельностью Пифагора .

Развивающая – учить детей рассуждать, выдвигать гипотезы и разрешать их, изобретать, анализировать, сравнивать, то есть активизировать их процесс мышления.

Оборудование к уроку:

1. компьютер, м/м установка , инструменты,

2. презентации,

3. газета о “Пифагоре”,

4. модели, верёвка, .

Структурный элемент урока

Используемые методы

Роли преподавателя

Позиции учащихся

Результат

Погружение

ЗУХ, проблемное обучение.»мозговой штурм»

Проектировщик и организатор проблемной творческой ситуации

Субъект групповой творческой деятельности

Таблица с частично заполненными столбцами

Осмысление

Частично-поисковый

метод, .»мозговой штурм»

Модератор

Субъект самостоятельной учебно-исследовательской деятельности

Самостоятельно доказанная теорема

Закрепление

Частично-поисковый

метод

Консультант

Субъект самостоятельной учебно-исследовательской деятельности

Изобретение инструмента

Рефлексия

ЗУХ

Эксперт

Субъект самостоятельной проектной деятельности

Таблица с заполненными столбцами

Ход урока

1. Организационный момент.(Погружение)

Здравствуйте ,дети. Прежде чем начать урок, я хочу увидеть вашу готовность к уроку: сколько предметов у вас на парте?

Мне интересно, какое у вас настроение?

Хорошо , теперь можно начинать урок . В тетради построим таблицу из трёх колонок.

В конце урока она должна быть заполнена.

Знаю

Хочу узнать

Узнал

Теперь давайте поиграем. Представьте , что мы попали на необитаемый остров, что бы нас спасти , лётчик поставил условие что бы взлётная площадка была строго прямоугольной формы и с размерами 30м. на 40м.Вы считаете, что это просто, давайте повторим тот материал , который нам понадобиться при решении данной задачи и заполним колонки таблицы.(слайд)

У нас возникла проблемная ситуация : чтобы построить прямоугольник надо построить прямой угол., Как?

— Давайте разберемся в ситуации, исследуем её, и определим, что надо знать , что бы справиться с проблемой..

2. Новый материал. (Осмысление)

Пришли к выводу , что нам не хватает знаний, даю вам подсказку в виде Т. Пифагора.

Открываем учебник на странице 126 и читаем предложенную формулировку теоремы Пифагора:

“В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов”.

Таким образом подошли к теме урока, которую вы без труда сформулируете сами.

Открываем тетради и записываем тему урока » Теорема Пифагора»(слайд)

Эпиграфом к уроку я выбрала слова И.Кеплера «…Геометрия владеет двумя сокровищами – теоремой Пифагора и золотым сечением….»(слайд)

С одним из сокровищ мы и будем с вами работать.Но прежде чем с этой теоремой работать м ыдолжны быть уверены, что она правильная. Пифагор её доказал , теперь попробуем доказать и мы.

Проведём практическую работу , постройте с помощью циркуля и линей прямоугольный треугольник по двум катетам ( 1-ряд :3 и 4, 2ряд: 6 и 8 , 3ряд:4.5 и 6) (слайд)

1.Измерьте гипотенузу.

2.Запишите в строчку данные. 3 4 5

6 8 10

4,5 6 7,5

3.Возведите в квадрат все значения.

4. Найдите закономерность. ( )

5.Кто сможет сделать вывод?( В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов

А какой треугольник мы рассматриваем? ( Да., эта теорема только для прямоугольных треугольников.)

Вернёмся к нашей задаче. Скажите, чему же будет равна диагональ нашего прямоугольника? ( 5 м.)

Следовательно нам сейчас достаточно построить прямоугольный треугольник и половина прямоугольника построен. Не просто так вам дана верёвка. С помощью этой верёвки и Т. Пифагора изобретите устройство, которое позволит нам проверить , что построенный угол прямой. Работа в группах 1 и 2 парта, 3и 4парты и т. Д.)

Да. Правильно. Это устройство носит название «Египетский треугольник»

Истор. справка: Землемеры Древнего Египта для построения прямого угла пользовались следующим приёмом. Бечёвку узлами делили на 12 равных частей и концы связывали. Затем бечёвку растягивали на земле так, что получался треугольник со сторонами 3, 4 и 5 делений. Угол треугольника, противолежащий стороне с 5 делениями, был прямой. ) В связи с указанным способом построения прямого угла треугольник со сторонами 3, 4 и 5 ед. иногда называют египетским.(слайд)

Интересна история Т. Пифагора.

Хотя эта теоремами связывается с именем Пифагора, она была известна задолго до него. В Вавилонских текстах эта теорема встречается за 1200 лет до Пифагора. Возможно , что тогда ещё не знали её доказательства , а соотношение между гипотенузой и катетами было установлено опытным путём на основе измерений. Пифагор по видимому нашёл доказательство этого соотношения. Сохранилось древнее предание, что в честь своего открытия Пифагор принёс в жертву богам быка, по другим свидетельствам 100 быков (слайд)

На протяжении последующих веков были найдены ещё более 100 доказательств.

Вернёмся к задаче, теперь вы без труда построите прямоугольник и сможете доказать, что угол у фигуры построен правильно.

Для закрепления теоремы решите следующие задачи. Теорема Пифагора имеет большое практическое значение. Очень часто она применяется при решении задач и чтобы решать сложные задачи, надо научиться решать задачи простые. Я предлагаю вам задачи, в которых надо найти неизвестные катет или гипотенузу, используя теорему.

Задача 1.Заполнить таблицу.

Задача 2. Найти х.

Задача3: В равнобедренном треугольнике АВС с основанием АС=16см. высота ВН=6см.Найдите боковую сторону.

Задача 4. Используя данный рисунок докажите Т. Пифагор

Историческая справка «Теорема Невесты»

3. Итоги урока. (Рефлексия)Наш урок подходит к концу. Осталось подвести итог. Для этого вернёмся к таблице ЗУХ и заполним третью колонку.

Узнали: терему Пифагора, её применение, о Пифагоре, как построить прямой угол.

1. Домашнее задание. 1. Найти ещё 3 доказательства теоремы.

2.Придумать задачу, в решении которой применяется

Т. Пифагора.